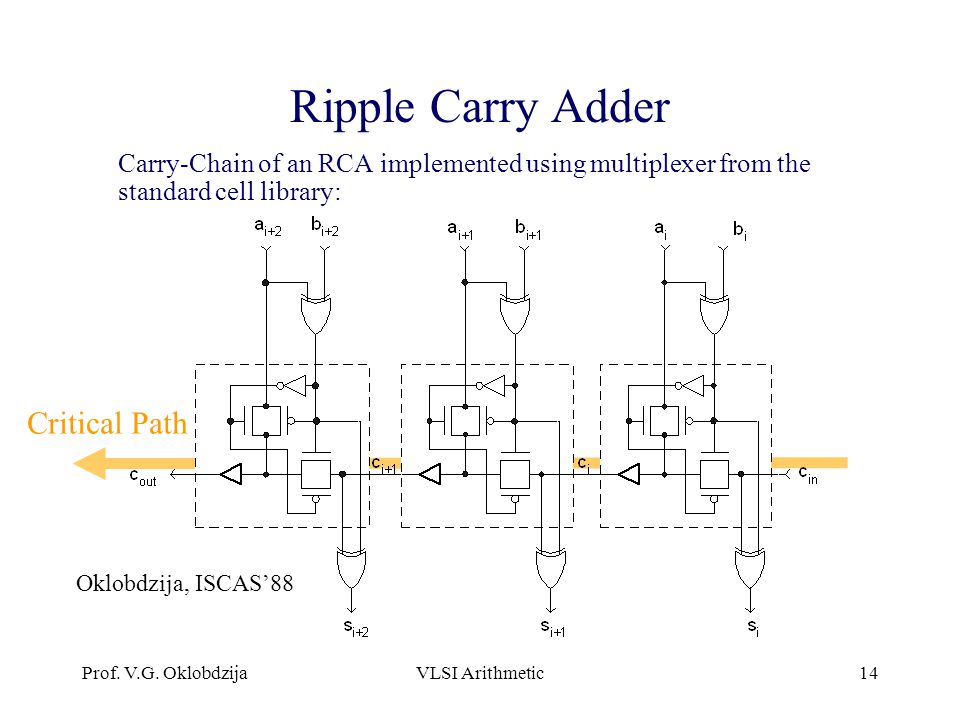
8 bit ripple carry adder critical path resources

The width of the first RCA is given as where is the arrival delay of the carry output from the previous block. The width of all remaining higher order RCAs in the same block will be 1 bit less because of the delayed arrival times of their carry input by an additional time unit. For a target delay of 6 time units, the width of the first RCA in is 4 bits and the widths of the remaining RCAs are each 3 bits. The number of RCAs in is limited to 3 due to the fan-in restriction of 7 on the skip logic.

A detailed block diagram of the first three blocks of the bit adder an expanded view of Figure 2 is shown in Figure 3. The three blocks together form a bit adder. Next let us consider the final block of the bit adder. Block is divided into a number of subblocks.

The maximum number of subblocks is again limited to 3 due to the fan-in restrictions on the skip logic. A block diagram of with an expanded view of subblock is shown in Figure 4. The subblock is further divided into RCAs. The number of inputs to the CG logic increases, successively, by 2 for each RCA and is limited to a maximum of 7 in any subblock.

Hence, the number of RCAs in any subblock is limited either by the number of inputs to the CG block or by the number of inputs to the block. Therefore, subblock 0 can accommodate 4 RCAs.

The carry input to the skip logic, as well as, to the first RCA arrives in 3 time units. The propagate and generate signals and from each RCA will be available with a delay of 1 time unit.

This implies that we can have two levels of logic inside the block while satisfying the time delay constraints. Hence, the total width of subblock is 9 bits. Figure 5 shows block with an expanded view of subblock The number of RCAs in is limited to 3 due to the condition stated earlier. The carry input to the first RCA of this subblock is given by. With an AOI logic implementation, will be available in 4 time units, thereby limiting the length of the first RCA to 2 bits.

The carry inputs and to the remaining RCAs in subblock are also available in 4 time units. Thus, the maximum width of subblock is 6 bits.

The carry input to the final subblock is given by. The maximum width of subblock can be calculated as 4 bits. Hence, the total width of block is 19 bits. By combining the 4 blocks and a bit adder can be implemented. The width of subblock can be shortened to 3-bits for a bit adder. The carry out from the skip logic is given by where,. An OAI logic implementation generates in 4 time units. A detailed block diagram of block is shown in Figure 6.

The final breakdown of the bit adder into 4 blocks is shown in Figure 7. A reduction in hardware can be achieved by moving subblock from block and placing it as another block This will eliminate 1 carry generate logic OAI and logic. Although our adder has already achieved the bit requirement, we still have room to extend the width further, while keeping the target delay the same. The schemes for the th and th blocks are shown in Figure 8. The fifth block is divided into three subblocks.

The subblocks have the same structure as block Since the carry fed into the th block has 4 unit delays, the maximum width of the first RCA will be 2 bits. The remaining RCAs will be 1 bit each. Thus, the maximum width for the fifth block will be 20 bits. The first subblock 11 bits is divided into subblocks of 5, 3, 2, and 1 bit. The subblock 6 bits is divided into 3 subblocks of 3, 2, and 1 bit.

Similarly, the final subblock 3 bits is divided into subblocks of 2 and 1 bit. The first 5-bit subblock consists of a 2-bit RCA and 3 individual full adders. Individual full adder cells form all other subblocks.

The th block is a single bit full adder. Thus, the total width of the adder becomes Based on the adder design procedure, we can derive a formula for calculating the maximum number of full adders in every block. The following notations are used in the derivation. For any block , the number of RCAs is defined by a recursive function. The recursive function is not valid for the blocks and , and the values for and when used in the recursive function are assumed to be zero The width of an RCA is defined in terms of the target delay.

The carry input to the first RCA of the block can be obtained directly from the previous carry-skip stage. Hence, the calculation of width for the first block is done differently from the others. The maximum number of full adders in block is given by. Table 1 lists the maximum adder size for a given target delay using our design procedure. A few basic CMOS cells are used for the design of the adder stage. The 3-input and 5-input cells are implemented in a straightforward manner, and are given by the following Boolean expressions: When the 7-input AOI and OAI cells are implemented in the above manner, the delay is prohibitive and hence we decided to implement them as a cascade connection of a number of smaller modules.

Their corresponding Boolean expressions are given by where and are the inputs to the cells. The full adder cell used in our design is the low-energy CMOS adder cell presented in [ 10 ]. The adder was implemented using Tanner tools pro L-edit was used to generate the layout and T-spice was used for performing the simulation. From Table 2 , it may be noted that the 5 and 7-input cell delays are comparable to that of the FA, while the 3-input cells have a much less delay.

The average power was measured by feeding 10, random vectors at a frequency of ? MHz and is also shown in Table 2. For comparison purposes, we selected two other types of adders. They are i bit carry skip-adder proposed in [ 4 ] and ii bit multilevel carry-skip adder proposed in [ 11 ].

The first one is referred here as Chirca adder and the second one is referred as Gayles adder. These adders were compared with our bit adder by measuring the critical path delays. To get a more realistic estimation of the delays involved, we laid out the complete bit adder stages and performed TSPICE simulation. The simulation was carried out at a frequency of ? The simulation results are shown in Table 3. These results show that our bit adder has the minimum delay of 3. The Chirca adder had a delay of 4.

Our bit adder was then extended to a bit adder with marginal delay increase, and these simulation results are also included in Table 3. Even this bit adder is found to be faster than the bit Gayles adder. The power consumption showed a marginal increase of power for our adder compared to Gayles adder while outperforming Chirca adder.

Overall, our bit adder achieved the lowest power-delay product. In this paper, we presented a new bit adder using carry-skip logic. The adder was implemented by dividing the adder into several blocks. The size of each block is limited by the delay of the carry-in signal and the final target delay. An algorithm is used to calculate the maximum size of the adder satisfying the target delay. The delay of a full adder is used as the unit of measurement in our analysis.

The adder has been implemented by generating the layout with Generic 0. MHz and supply voltage of 3. V showed a critical path delay of 3. The comparison results show that our adder is faster than Chirca and Gayles carry-skip adders. Furthermore, a bit adder implemented using our approach can operate almost at the same speed as a bit Chirca adder or Gayles adder.

Even though our adder has a marginal increase in power consumption compared to the Gayles adder, overall, we achieved the lowest power-delay product. Home Journals About Us. Indexed in Web of Science. Subscribe to Table of Contents Alerts. Table of Contents Alerts. Abstract The design of a bit carry-skip adder to achieve minimum delay is presented in this paper.

Introduction The ever-increasing demand for mobile electronic devices requires the use of power-efficient VLSI circuits.

Theoretical Background and Previous Work The design of a carry-skip adder is based on the classical definition of generate and propagate signals as follows [ 1 , 2 ]: Then, the expression for carry out from the whole group is given by Different adder implementations have been developed to optimize various design parameters.

The algorithm ends up in an unbalanced binary tree with a delay of consuming an area The ELM-adder design presented in [ 7 ] computes the sum bits in parallel; thereby reducing the number of interconnects. The bit adder divided into 4 blocks [ 4 ]. Block schematics for first three blocks of bit adder. Detailed view of the first three blocks of bit adder. Task 3 This task is mandatory Design a ripple-carry adder that adds two 8-bit numbers. A ripple-carry adder is composed of 1-bit full adders: What is the delay of the critical path?

It is assumed that initially both inputs are 0 and they change value cleanly and simultaneously to the values mentioned above. What if this was not the case? With what clock frequency can this adder be used to calculate sums?

And yes, the system really has separate w inputs. Use the technology specified in the table below. The delay of the critical path must not exceed 1. Try to achieve a result with small area within the timing restrictions. He received the B.